Nucleotide diversity

We define nucleotide diversity (\(\pi\)) as the probability that two alleles are heterozygous at a random nucleotide position in the genome.

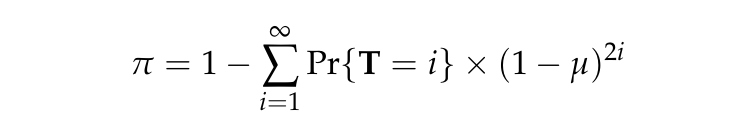
where T is a random variable representing time to coalescence and \(\mu\) is the single nucleotide substitution rate. From empirical observations we estimate that \(\mu = 1.1 \times 10^{-8}\) per generation.

We evaluate the above expression by using coalestr as follows:

1. We create a Population by specifying its transmission history.

2. We use get_coalescent to obtain the probability distribution of T.

3. We use get_diversity to evaluate the above summation series.

!pip install coalestr
from coalestr import cs

''' We create a history of transmission parameters 
which in this case are constant over time

my_history = [[D, N, Q, X, M]]

   D = duration of simulation
   N = effective number of hosts (Nh)
   Q = quantum of transmission
   X = crossing rate of transmission chains (chi)
   M = number of migrant hosts (Nm) '''

my_history = [[100000, 18764, 1, 0, 0]]
my_population = cs.Population(my_history)
my_population.get_coalescent()
my_population.get_diversity()

Observation time.    Events captured.   Mean coalescence time
                      beho      wiho        beho     wiho
        0              99.5     100.0     18188.4      1.0
Observation time.    SNP heterozygosity.   Haplotype homozygosity at 27.0 kb locus
                      beho       wiho           beho       wiho
        0           4.00e-04   2.20e-08       4.09e-03   9.87e-01

This tells us that for between-host (beho) comparisons, i.e. sampling from different hosts:

• Our simulation captures 99.5% of coalescent events

• Mean coalescence time is 18188.4 generations

• Nucleotide diversity (aka SNP heterozygosity) is \(4 \times 10^{-4}\)

For within-host (wiho) comparisons, i.e. sampling from the same host:

• Our simulation captures 100% of coalescent events

• Mean coalescence time is 1 generation

• Nucleotide diversity (aka SNP heterozygosity) is \(2.2 \times 10^{-8}\)

Haplotype homozygosity is discussed elsewhere.

In the following cells we will look at other combinations of transmission parameters that give us the same level of between-host nucleotide diversity, i.e. \(\pi = 4 \times 10^{-4}\) (which is approximately the level seen in the global parasite population).

def my_pop (D, N, Q, X, M):
    pop = cs.Population(history = [[D, N, Q, X, M]])
    pop.get_coalescent()
    pop.get_diversity()

my_pop(100000, 18754, 10, 0, 0)
# N = 18754, Q = 10, X = 0

Observation time.    Events captured.   Mean coalescence time
                      beho      wiho        beho     wiho
        0              99.5     100.0     18188.8     10.0
Observation time.    SNP heterozygosity.   Haplotype homozygosity at 27.0 kb locus
                      beho       wiho           beho       wiho
        0           4.00e-04   2.20e-07       3.67e-03   8.85e-01

my_pop(100000, 18754, 1, 0.5, 0)
# N = 18754, Q = 1, X = 0.5

Observation time.    Events captured.   Mean coalescence time
                      beho      wiho        beho     wiho
        0              99.5      99.8     18180.0   9091.0
Observation time.    SNP heterozygosity.   Haplotype homozygosity at 27.0 kb locus
                      beho       wiho           beho       wiho
        0           4.00e-04   2.00e-04       4.09e-03   4.96e-01

my_pop(100000, 5568, 10, 0.5, 0)
# N = 5568, Q = 10, X = 0.5

Observation time.    Events captured.   Mean coalescence time
                      beho      wiho        beho     wiho
        0              99.5      99.6     18188.9  14213.0
Observation time.    SNP heterozygosity.   Haplotype homozygosity at 27.0 kb locus
                      beho       wiho           beho       wiho
        0           4.00e-04   3.13e-04       3.99e-03   2.14e-01

my_pop(100000, 3269, 10, 1, 0)
# N = 3269, Q = 10, X = 1

Observation time.    Events captured.   Mean coalescence time
                      beho      wiho        beho     wiho
        0              99.5      99.6     18187.4  16687.4
Observation time.    SNP heterozygosity.   Haplotype homozygosity at 27.0 kb locus
                      beho       wiho           beho       wiho
        0           4.00e-04   3.67e-04       4.05e-03   8.44e-02