Transient scenarios

Here we model a local subpopulation of parasites that in steady state has \(N_h = 10\), \(Q = 5\), \(\chi = 0\). Despite its small size, the local subpopulation maintains a fairly high level of nucleotide diversity \(\pi_S \approx 3 \times 10^{-4}\) due to a constant rate of migration \(N_m = 1\) from the global metapopulation. We construct a toy model of the global metapopulation using the coalestr.species function.

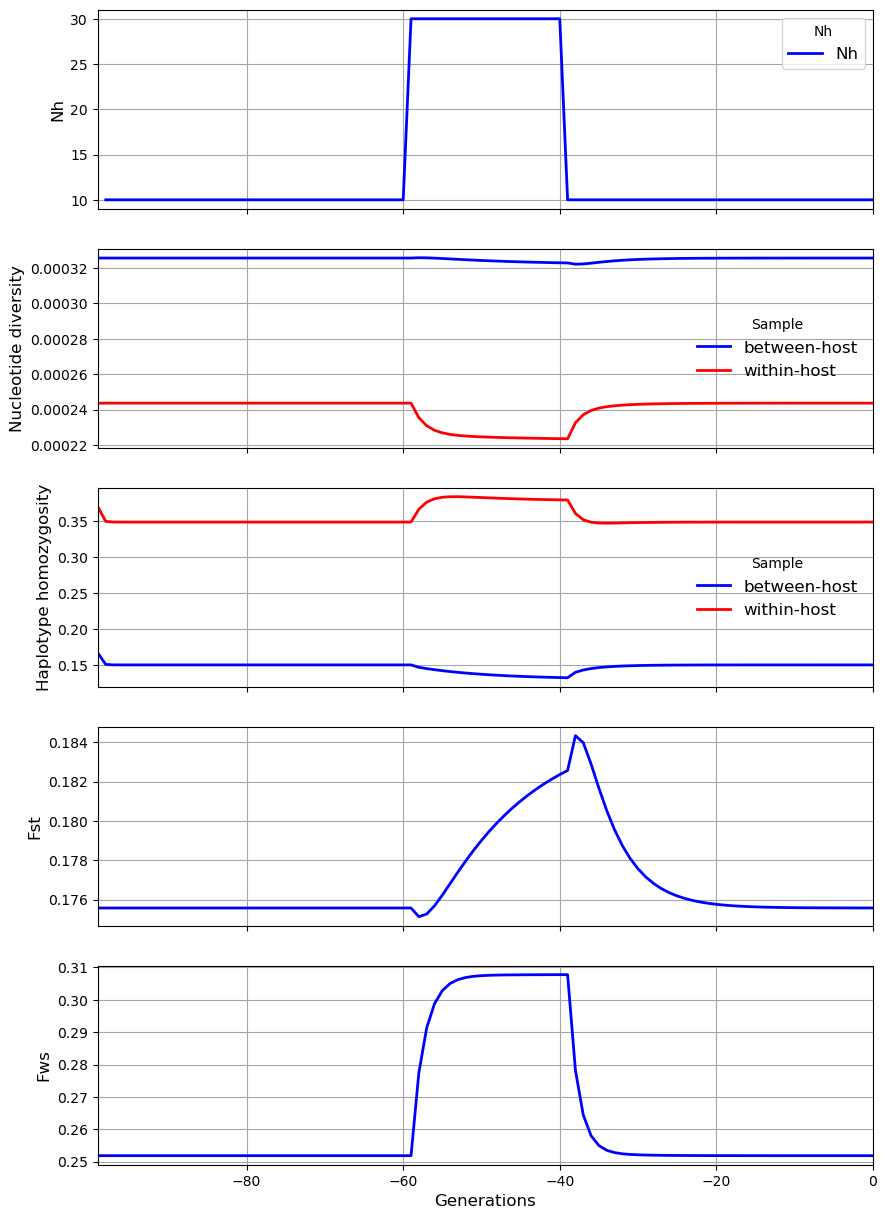
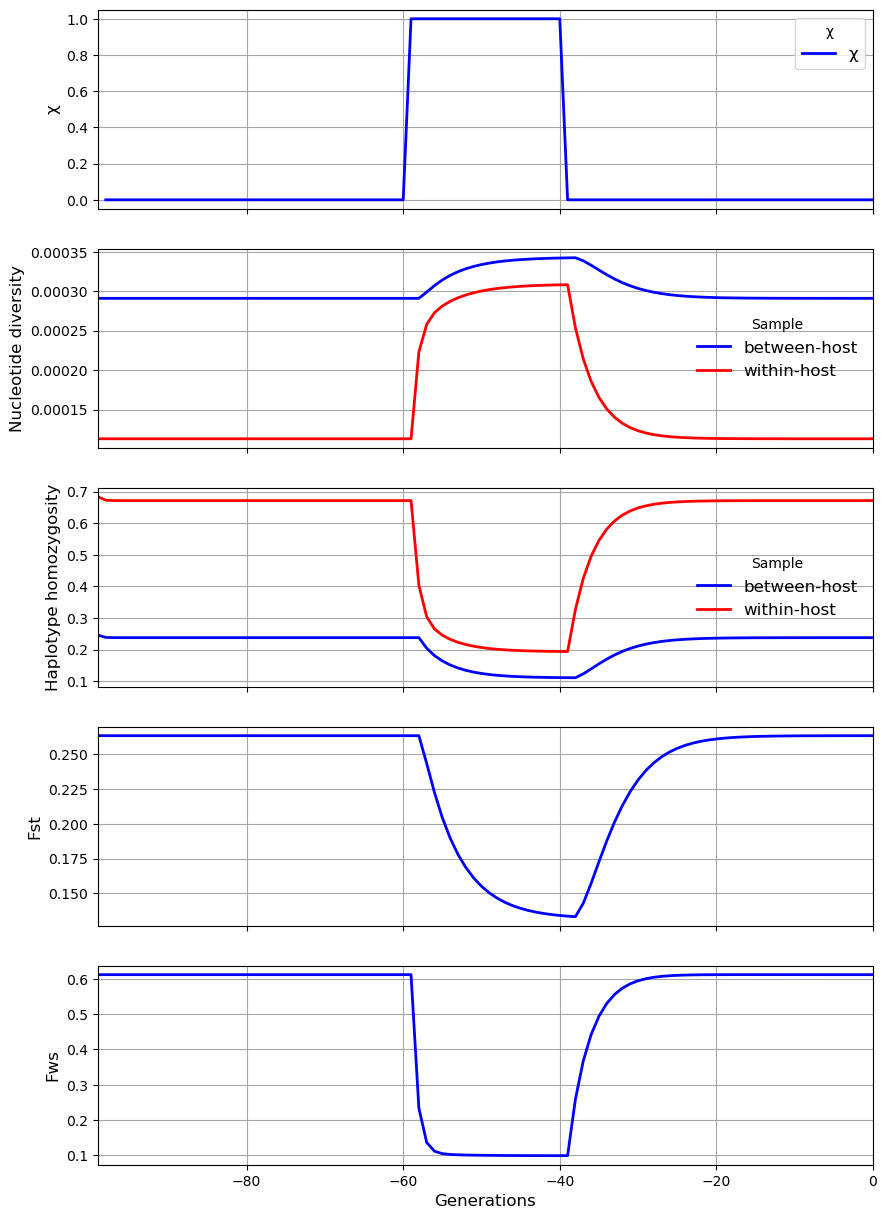
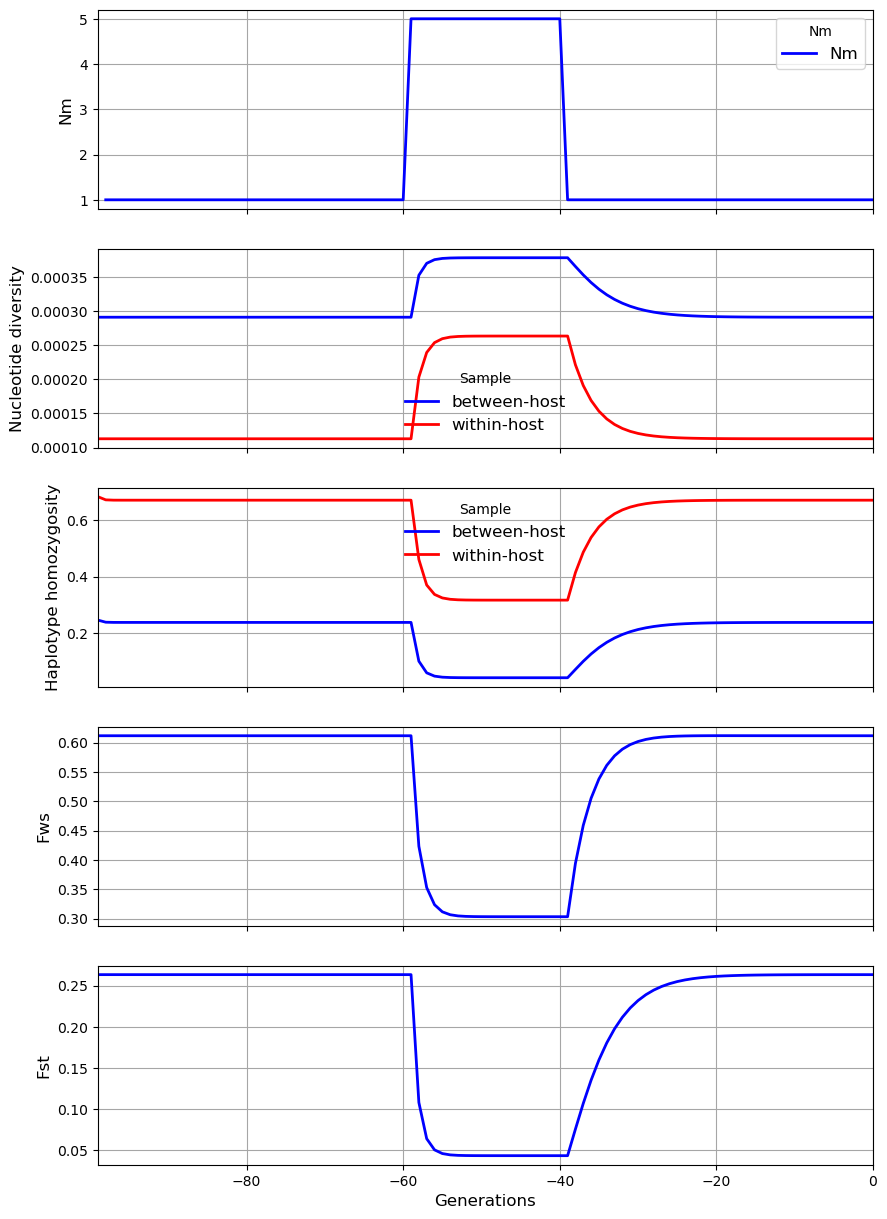
We simulate a step change in transmission parameters that starts 60 generations (15 years) before the present and lasts 20 generations (5 years). We examine the effects on nucleotide diversity of the subpopulation \(\pi_S\), mean within-host nucleotide diversity \(\pi_W\), haplotype homozygosity of the subpopulation at a 2cM locus \(\gamma_S\), mean within-host haplotype homozygosity at a 2cM locus \(\gamma_W\), the fixation index \(F_{ST}\) and the inbreeding index \(F_{WS}\).

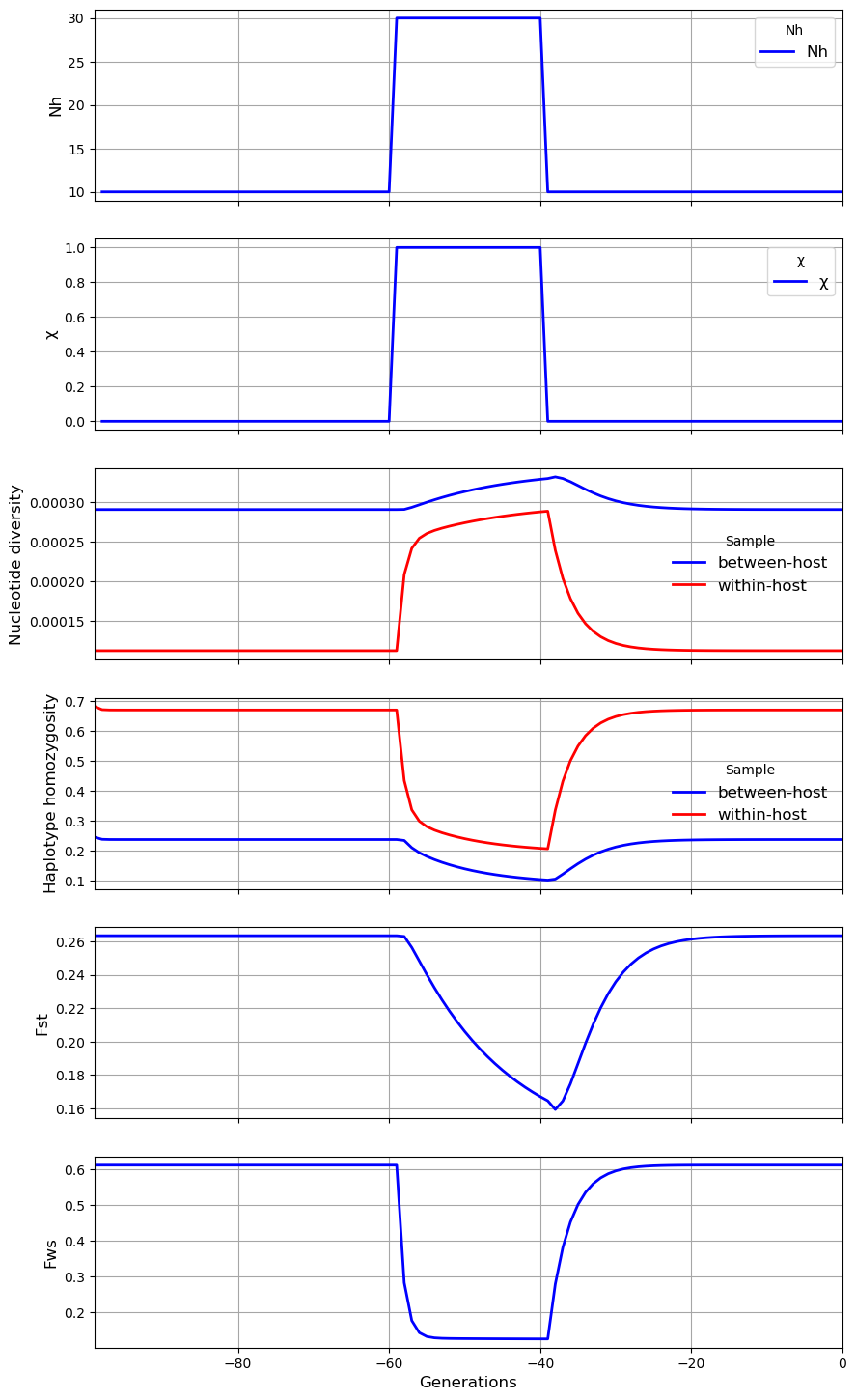
1. In the first scenario, the level of \(\chi\) in the subpopulation transiently increases from 0 to 1. The result is a sharp rise in \(\pi_W\) and a sharp fall in \(\gamma_W\), \(F_{ST}\) and \(F_{WS}\). There is also a modest rise in \(\pi_S\) and a modest fall in \(\gamma_S\).

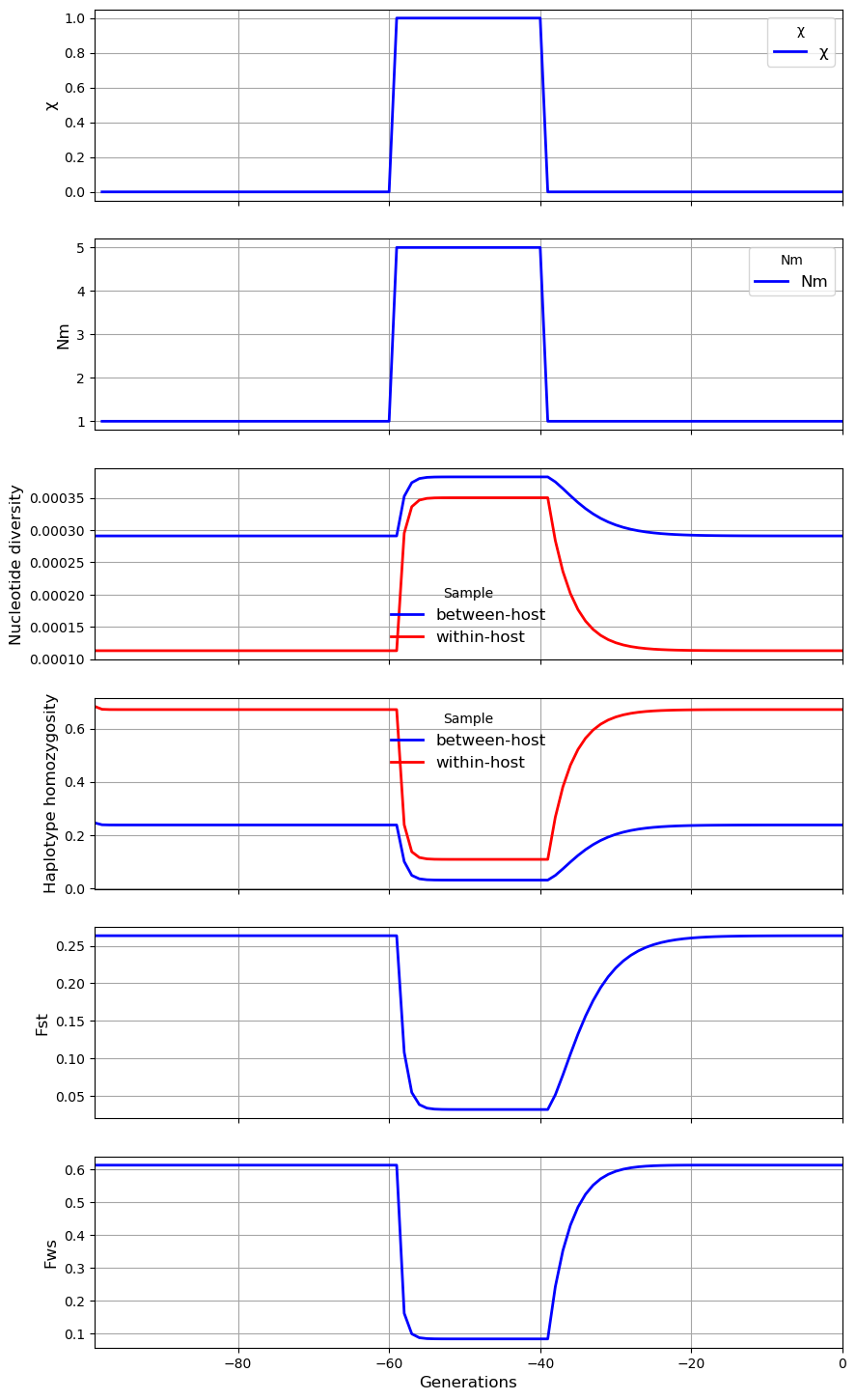
2. In the second scenario, the rate of migration \(N_m\) from the metapopulation into the subpopulation transiently increases from 1 to 5. This causes a sharp rise in \(\pi_W\), a more modest rise in \(\pi_S\) and a sharp fall in \(\gamma_W\), \(\gamma_S\), \(F_{ST}\) and \(F_{WS}\). Thus the effects of an increase in \(N_m\) are rather similar to those of an increase in \(\chi\).

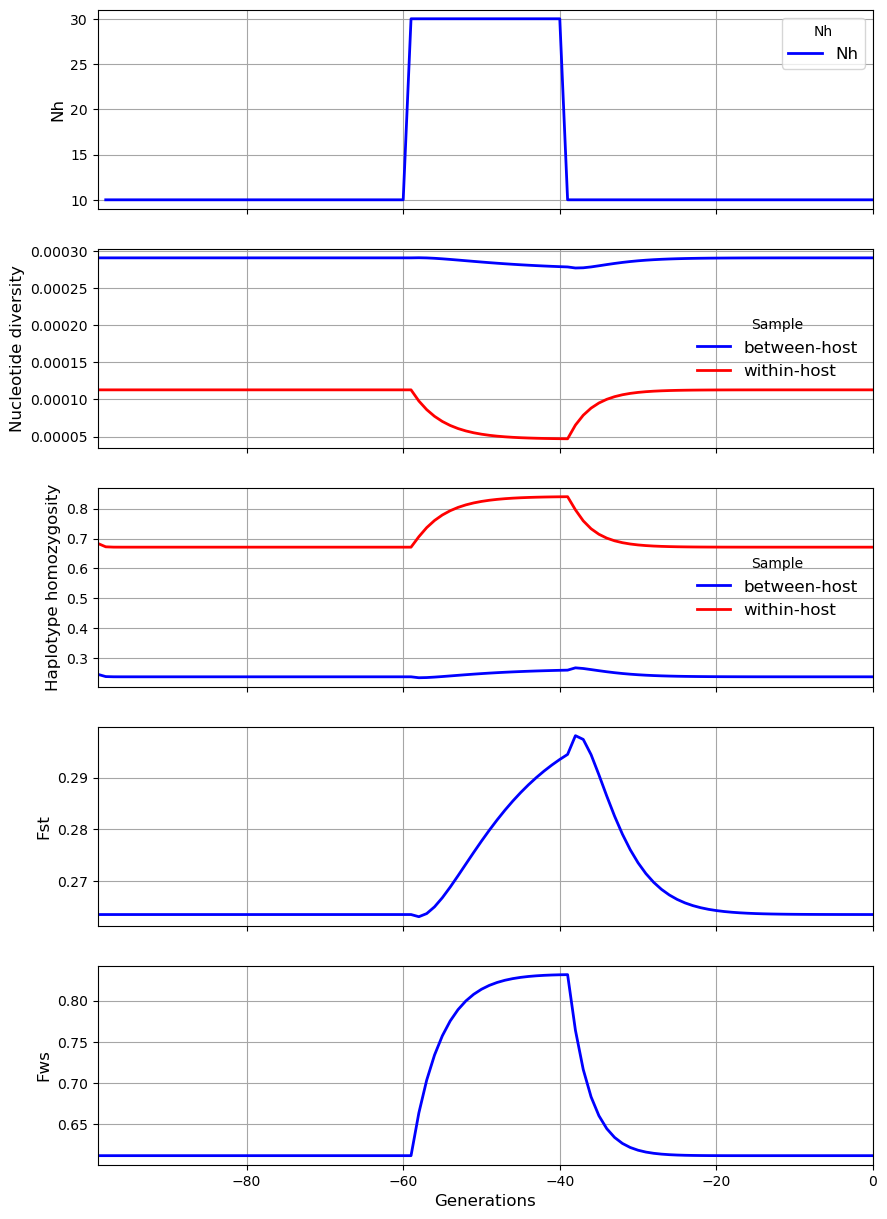
3. In the third scenario, the level of \(N_h\) in the subpopulation transiently increases from 10 to 30. The result is a sharp rise in \(F_{WS}\), a modest rise in \(F_{ST}\) and \(\gamma_W\), a modest fall in \(\pi_W\), and small reduction in \(\pi_S\). These results appear paradoxical because we might expect an increase in \(N_h\) to cause \(\pi_S\) to rise whereas it falls slightly. The paradox can be explained by recalling that \(N_m = mN_h\). Although \(N_m\) is constant, the rise in \(N_h\) causes \(m\) to decline, and this reduction in the proportion of hosts that have migrated from the metapopulation counterbalances the local increase in effective number of hosts, causing \(\pi_S\) to remain almost unchanged.

We also look at more complex scenarios involving step changes in a combination of transmission parameters.

!pip install coalestr
from coalestr import cs

metapop = cs.species()
metapop.get_coalescent()
metapop.get_diversity()

Observation time.    Events captured.   Mean coalescence time
                      beho      wiho        beho     wiho
        0             100.0     100.0     17961.7   6421.2
Observation time.  Nucleotide diversity     Haplotype homozygosity
                      beho       wiho           beho       wiho
        0           3.95e-04   1.41e-04       3.23e-03   5.92e-01

''' 
Steady state: N=10, Q=5, X=0, M=1
Transient scenario: X=1 for 20 generations
'''

subpop_history = [[300, 10, 5, 0, 1],
                  [20, 10, 5, 1, 1],
                  [40, 10, 5, 0, 1]]

observations = range(100)

subpop = cs.Population(subpop_history, metapopulation = metapop)
subpop.get_coalescent(observations, show = False)
subpop.get_diversity(show = False)
subpop.plot_observations(metrics = ("X", "snp_het", "hap_hom", "Fst", "Fws"))

''' 
Steady state: N=10, Q=5, X=0, M=1
Transient scenario: M=5 for 20 generations
'''

subpop_history = [[300, 10, 5, 0, 1],
                  [20, 10, 5, 0, 5],
                  [40, 10, 5, 0, 1]]

observations = range(100)

subpop = cs.Population(subpop_history, metapopulation = metapop)
subpop.get_coalescent(observations, show = False)
subpop.get_diversity(show = False)
subpop.plot_observations(metrics = ("M", "snp_het", "hap_hom", "Fws", "Fst"))

''' 
Steady state: N=10, Q=5, X=0, M=1
Transient scenario: N=30 for 20 generations
'''

subpop_history = [[300, 10, 5, 0, 1],
                  [20, 30, 5, 0, 1],
                  [40, 10, 5, 0, 1]]

observations = range(100)

subpop = cs.Population(subpop_history, metapopulation = metapop)
subpop.get_coalescent(observations, show = False)
subpop.get_diversity(show = False)
subpop.plot_observations(metrics = ("N", "snp_het", "hap_hom", "Fst", "Fws"))

''' 
Steady state: N=10, Q=5, X=0, M=1
Transient scenario: N=30, X=1 for 20 generations
'''

subpop_history = [[300, 10, 5, 0, 1],
                  [20, 30, 5, 1, 1],
                  [40, 10, 5, 0, 1]]

observations = range(100)

subpop = cs.Population(subpop_history, metapopulation = metapop)
subpop.get_coalescent(observations, show = False)
subpop.get_diversity(show = False)
subpop.plot_observations(metrics = ("N", "X", "snp_het", "hap_hom", "Fst", "Fws"))

''' 
Steady state: N=10, Q=5, X=0, M=1
Transient increase of X=1, M=5 for 20 generations
'''

subpop_history = [[300, 10, 5, 0, 1],
                  [20, 10, 5, 1, 5],
                  [40, 10, 5, 0, 1]]

observations = range(100)

subpop = cs.Population(subpop_history, metapopulation = metapop)
subpop.get_coalescent(observations, show = False)
subpop.get_diversity(show = False)
subpop.plot_observations(metrics = ("X", "M", "snp_het", "hap_hom", "Fst", "Fws"))

''' 
Steady state: N=10, Q=5, X=0.5, M=1
Transient increase of N=30 for 20 generations
'''

subpop_history = [[300, 10, 5, 0.5, 1],
                  [20, 30, 5, 0.5, 1],
                  [40, 10, 5, 0.5, 1]]

observations = range(100)

subpop = cs.Population(subpop_history, metapopulation = metapop)
subpop.get_coalescent(observations, show = False)
subpop.get_diversity(show = False)
subpop.plot_observations(metrics = ("N", "snp_het", "hap_hom", "Fst", "Fws"))